Mathematicians Pioneer New Approach to Solve Complex Algebraic Equations

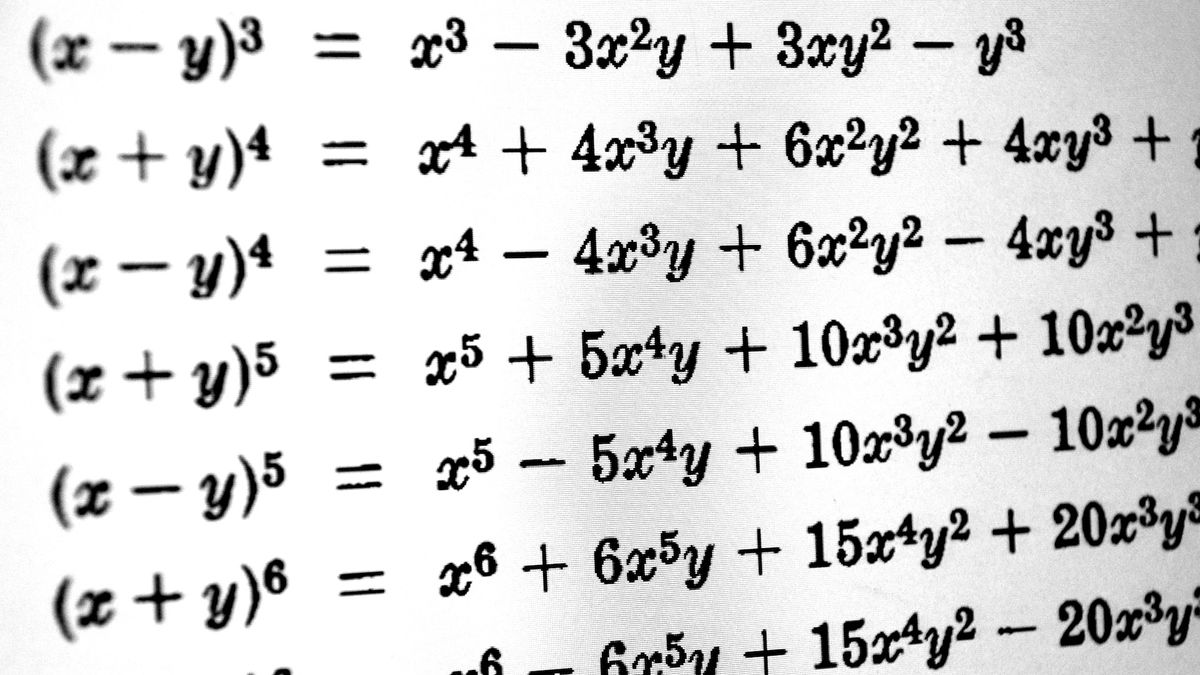
Quick Summary

• Mathematician Norman Wildberger (University of New South Wales) and autonomous computer scientist Dean Rubine have developed the first general method for solving high-order polynomial equations.
• Their study, published April 8 in The American Mathematical Monthly, introduces a new approach that avoids relying on irrational numbers or radicals.
• Polynomial equations involve algebraic expressions with variables raised to non-negative powers; solving simple polynomials is widely understood, but higher-order polynomials (x⁵ and beyond) remain challenging due to infinite solutions through radicals.
• The researchers utilized polynomial extensions called power series, commonly used in geometric problems within combinatorics math.
• They focused on higher analogues of catalan numbers-a sequence historically linked to mathematical operations on polygons-and termed their methodology “the Geode.”
• Potential applications for the Geode include advancements in computer science and graphics. Wildberger described the development as “a dramatic revision of a basic chapter in algebra.”

Indian Opinion Analysis

This breakthrough represents a pivotal shift within mathematical sciences by offering solutions previously deemed infeasible. For India-a nation deeply invested in STEM education and technological innovation-developments like this hold notable potential to bolster academic research opportunities and provide novel approaches within sectors utilizing advanced computing, such as data analytics or artificial intelligence.

India’s emphasis on nurturing globally competitive mathematicians may benefit from integrating knowledge around methodologies like the Geode into its educational system. Moreover, this discovery could indirectly impact industries reliant on algorithm optimization, offering prospects for Indian tech companies operating at scale worldwide.

Read More